Reasoning capacities represent a fundamental component of AI systems. The introduction of OPENAI O1 aroused significant interest in building reasoning models thanks to learning approaches by large -scale strengthening (RL). While the opening of Deepseek-R1 has enabled the community to develop advanced reasoning models, critical technical details, including data conservation strategies and specific RL training revenues, have been omitted from the initial report. This absence has left researchers who find it difficult to reproduce success, leading to fragmented efforts exploring different model sizes, initial control points and target fields. Different model sizes, initial control points, distilled reasoning models, target areas, code and physical AI are explored, but lack of conclusive or coherent training recipes.
Training language models for reasoning focus on mathematical fields and code thanks to end-up and supervised pre-training adjustment approaches. RL's first attempts using specific reward models show limited gains due to challenges inherent in mathematical and coding tasks. Recent efforts after the Deepseek-R1 version explore rules-based verification methods, where mathematical problems require specific output formats for precise verification, and code problems use compilation and execution feedback. However, these approaches are focused on unique areas rather than managing heterogeneous guests, restricted reference assessments limited to love and Livecodebench, and training instability problems requiring techniques such as the length of progressive response increases and the attenuation of entropy.
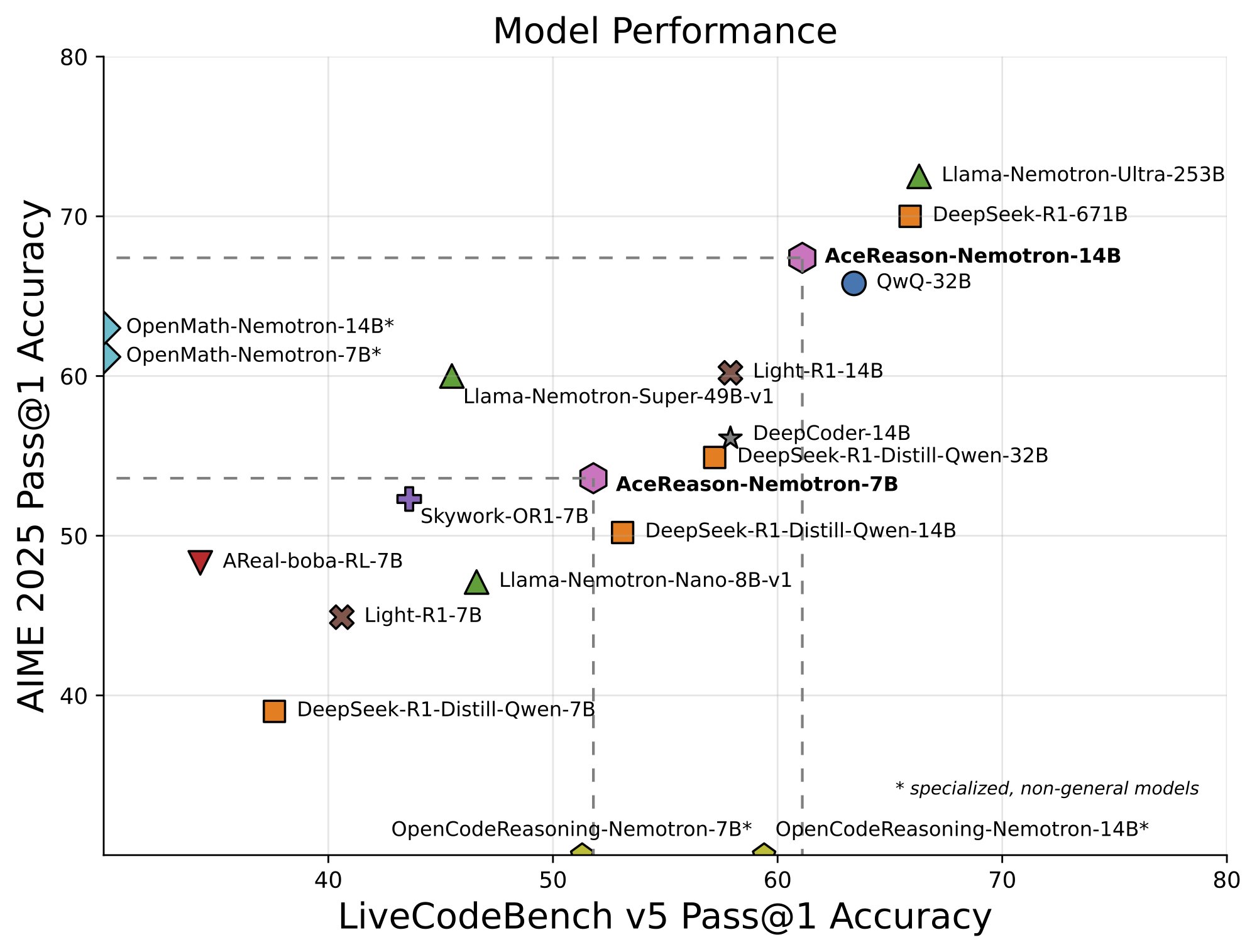
NVIDIA researchers demonstrate that large -scale RL can considerably improve the reasoning capacities of small and medium -sized models, surpassing approaches based on cutting -edge distillation. The method uses a simple but effective sequential training strategy: the conduct of an RL training first on invites in mathematics, followed by invites only. This reveals that the mathematical RL improves performance on mathematical references and improves code reasoning tasks, while the extensive iterations of the RL only increase the performance of the code with minimum degradation in mathematical results. In addition, a robust data storage pipeline is developed to collect difficult prompts with high -quality verifiable tests and test cases, allowing an RL based on verification in the two areas.
The method conducts data storage for RL in mathematics and RL only on the code. For RL only in mathematics, the pipeline merges the deepscal data sets and Numinamath covering algebra, combinatorics, numbers of numbers and geometry, applying 9 gram filtering and strict exclusion rules for inappropriate content. The Deepseek-R1 model validates questions through eight attempts, only retaining correct solutions voted by the majority via a rules based on rules. The data set for the RL only of the code is organized from modern competitive programming platforms using formats for calculating functions and STDIN / STDOUS on algorithmic subjects. In addition, researchers filter incompatible problems, complete test cases conserving on-board cases and attribute difficulty scores using a Deepseek-R1-671B assessment, producing 8,520 verified coding problems.
The results show that the Acereason-Nemotron-7b model is 14.5% and 14.6% on the AIM 2025/2025, with gains of 14.2% and 8% respectively on LiveCodebench V5 / V6 compared to the initial SFT models. Variant 14B surpasses larger models like Deepseek-R1-Distill-Qwen-32B and Deepseek-R1-Distill-Lalma-70B, obtaining the best class results among the open reasoning models based on RL. Compared to Sota Distillation-Based Models, Acereason-Nemotron-14b Outperforms OpenMath-14b/32b by 2.1%/4.4% We like benchmarks and OpenCodereasoning-14B by 1.7%/0.8% on Livecodebench, showing that rl Achieves Higher Performance DISTILLATION Approaches by Holding Competitive Performance Against Frontier Models Like QWQ-32B and O3-MINI.
In this article, researchers show that large -scale RL improves the reasoning capacities of high and medium -sized SFT models thanks to sequential training specific to the field. The proposed approach to the realization of RL in mathematics followed by invites only in code reveals that the training of mathematical reasoning considerably increases the performance between the mathematical and coding references. The data storage pipeline allows an RL based on verification in heterogeneous fields by collecting difficult prompts with high -quality verifiable tests and test cases. The results reveal that RL repels the model's reasoning limits, providing solutions to insoluble problems and establishing new performance references for the development of the reasoning model.
Discover the Paper And Model on the embraced face. All the merit of this research goes to researchers in this project. Also, don't hesitate to follow us Twitter And don't forget to join our 95K + ML Subdreddit and subscribe to Our newsletter.
Sajjad Ansari is a last year's first year of the Kharagpur Iit. As a technology enthusiast, he plunges into AI's practical applications by emphasizing the understanding of the impact of AI technologies and their real implications. It aims to articulate complex AI concepts in a clear and accessible way.