MIT researchers are developing methods to control the transformer’s sensitivity with limpschitz boundaries and mud

Training of large -scale transformers in a stable manner has been a long -standing challenge in in -depth learningEspecially since the models develop in size and expressiveness. MIT researchers attack a persistent problem with its root: the unstable growth in activations and peaks of loss caused by unconstusive weight and activation standards. Their solution is to apply Lipschitz bounds On the transformer by spectrally regulating weights – * without using activation standardization, QK standard or Logit Softcaping tips.

What is Lipschitz – and why apply it?

A Lipschitz linked On a neural network quantifies the maximum quantity by which the output can change in response to input disturbances (or weight). Mathematically, an FFF function is kkk -lipschitz if: ∥f (x1) −f (x2) ∥≤k∥x1 – x2∥ ∀x1, x2 | F (x_1) – F (x_2) | Leq K | x_1 – x_2 | For all x_1, x_2∥f (x1) −f (x2) ∥≤k∥x1 – x2∥ ∀x1, x2

• Lipschitz Bolan Good ⇒ Robustness and predictability more important.
• It is crucial for stability, adversary robustness, confidentiality and generalization, with lower limits, which means that the network is less sensitive to changes or contradictory noise.

Declaration of motivation and problem

Traditionally, the formation of large -scale stable transformers has involved A variety of “band-aid” stabilization stuff::

• Layer normalization
• QK standardization
• Logit Tanh Softcaping

But these do not directly deal with the underlying spectral growth (greater singular value) of weights, a deep cause of explosion of activations and the instability of training, especially in large models.

THE central hypothesis:: If we regulate the weights themselves spectrally – beyond optimizer or activations – we can maintain close control over lipschitzness, potentially resolving instability at its source.

Key innovations

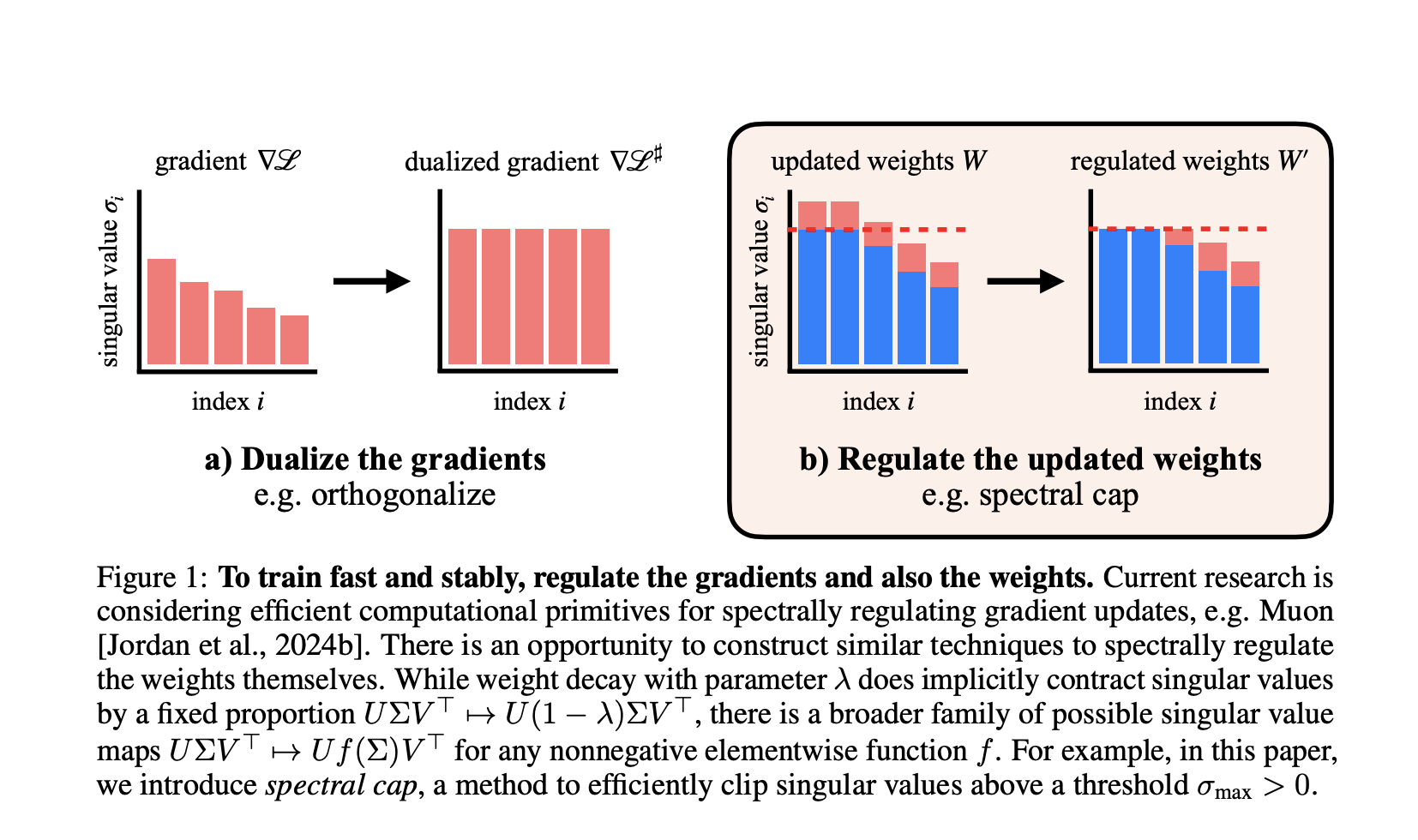
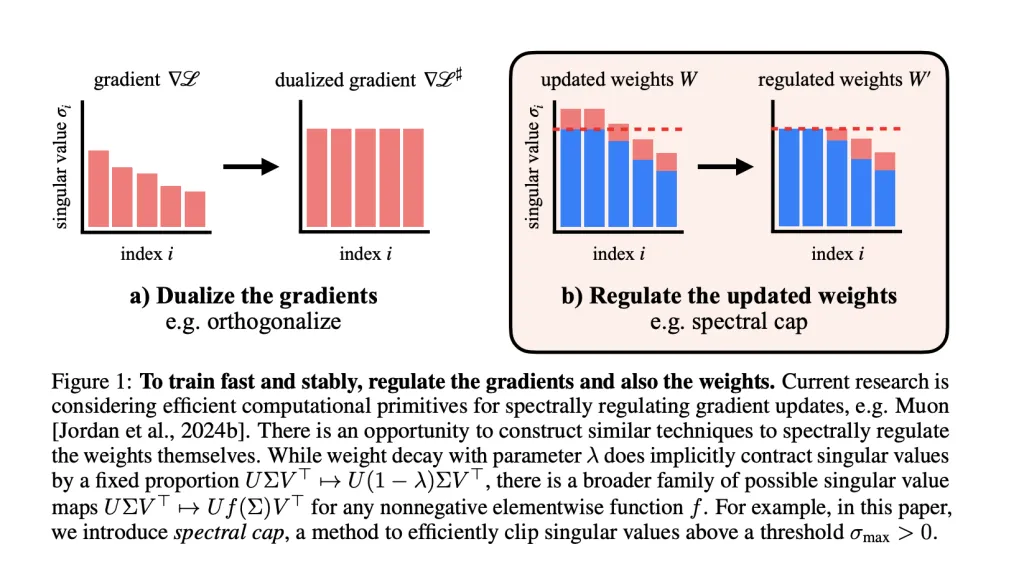
Spectral weight regulation and muon optimizer

• Muon Optimizer spectrally regularized gradientsGuarantee that each gradient step does not increase the spectral standard beyond a defined limit.
• Researchers Extend weight regulations: After each stage, they apply operations to Cape the singular values of each weight matrix. Activation standards remain remarkably small Consequently, rarely exceeding values compatible with the FP8 accuracy in their transformers on GPT-2 scale.

Delete stability tips

In all experiences, No layer normalization, no QK standard, no Tanh Logit was used. Again,

• Maximum activation entries in Their transformer on a GPT-2 scale has never exceeded ~ 100, While the basic line without constraint exceeded 148,000.

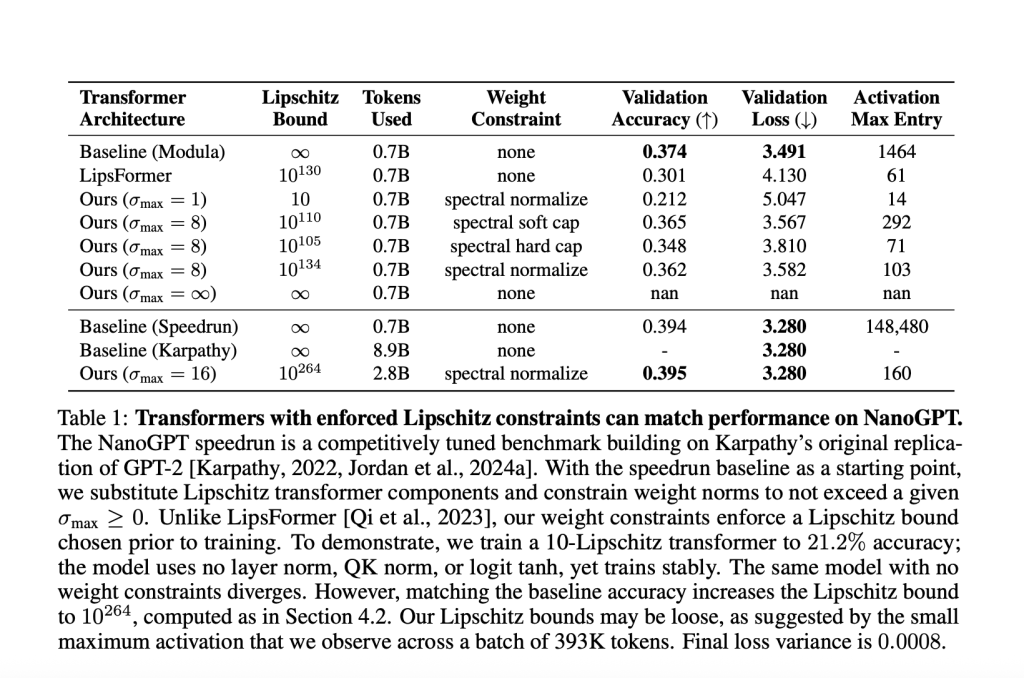
Table sample (Nanogpt experience)

Model	Maximum activation	Layer stability tips	Validation precision	Lipschitz linked
Baseline (speedrun)	148,480	Yes	39.4%	∞
Lipschitz transformer	160	None	39.5%	10¹⁰²⁶⁴

Methods to apply lipschitz constraints

A variety of Weight standard constraint methods were explored and compared for their ability to:

1. Maintain high performance,,
2. Guarantee a linked lipretteAnd
3. Optimize the performance-lipschitz compromise.

Techniques

• Weight decomposition: Standard method, but not always strict on the spectral standard.
• Spectral normalization: Guarantees that the higher singular value is capped, but can affect all singular values on a global scale.
• Spectral capture: New method, gently applies and effectively σ → min⁡ (σmax, σ) sigma to min (sigma_ {text {max}}, sigma) σ → min (σmax, σ) to all the singular values in parallel (using approximations of odd polynomial). This is co-conceived for stable updates at high level of muon for tight limits.
• Spectral hammer: Defines only the greatest singular value to σmaxSigma_ {text {max}} σmax, better suited to Adamw Optimizer.

Experimental results and ideas

Model assessment at different scales

1. Shakespeare (small transformer, <2-lipschitz):
   • Reaches a validation accuracy of 60% with a provable lipschitz linked below.
   • Surpass the basic line without constraint in the loss of validation.
2. Nanogpt (parameters 145m):
   • With a linked lipschitz <10, validation precision: 21.2%.
   • HAS match The strong non -constrained base (39.4% precision), requires a large upper limit of 1026410 ^ {264} 10264. This underlines how strict lipschitz constraints are that often compromise with large -scale expressiveness for the moment.

Efficiency of the weight constraint method

• Muon + captral spectral:: Leads the compromise border—The constants of lipschitz milder for loss of validation paired or better compared to the decrease in the Adamw +weight.
• Spectral capo-doux and normalization (Sous Muon) Constantly Activate the best border on the compromise Loss-Lipschitz.

Stability and robustness

• Opponent robustness Increases sharply to the lower limipschitz limits.
• In experiences, the models with a constrained lip constant suffered a much softer drop in precision in a contradictory attack compared to the baselines without constraint.

Activation size

• With spectral weight regulation: Maximum activations remain tiny (almost compatible) compared to unlimited basic lines, even on a large scale.
• This opens avenues to Low precision and inference training In the equipment, where smaller activations reduce the costs of calculation, memory and energy.

Limitations and open questions

• Selection of “tightest” compromise For weight standards, logit scaling and attention is always based on sweeping, not a principle.
• The higher link of the current is loose: The calculated global limits can be astronomically large (for example 1026410 ^ {264} 10264), while the actual activation standards remain low.
• It is not clear if basic performance correspondence without constraint with strictly small limipschitz limits is possible as the scale increases –More necessary research.

Conclusion

Spectral weight regulation – in particular when associated with Muon optimizer – can stable large transformers stable with forced lip limits, without standardization of activation or other band tips. This deals with instability at a deeper level and maintains activations in a compact and predictable beach, considerably improving opponent robustness and potentially material efficiency.

This work line points to effective new IT primitives for the regulation of the neural network, with large applications for confidentiality, security and deployment of low -precision AI.

---

Discover the Paper,, GitHub page And Face Project page Streced. Do not hesitate to consult our GitHub page for tutorials, codes and notebooks. Also, don't hesitate to follow us Twitter And don't forget to join our Subseubdredit 100k + ml and subscribe to Our newsletter.