The LLMs have shown notable improvements in mathematical reasoning by extending through natural language, causing performance gains on benchmarks such as mathematics and loves it. However, the learning of strengthening (RL) for the formation of these models encounters a challenge: the verification of the accuracy of the evidence of natural language is very difficult, requiring a careful manual verification of each step of reasoning. This limits the application of RL for the training of mathematical theorem supply models. While formal languages like Lean offer automatic verification of automatic accuracy, current LLM formal promoters are faced with their limits. The promotions of level level generate code gradually, but require special scaffolding and lack high level reasoning capacities.
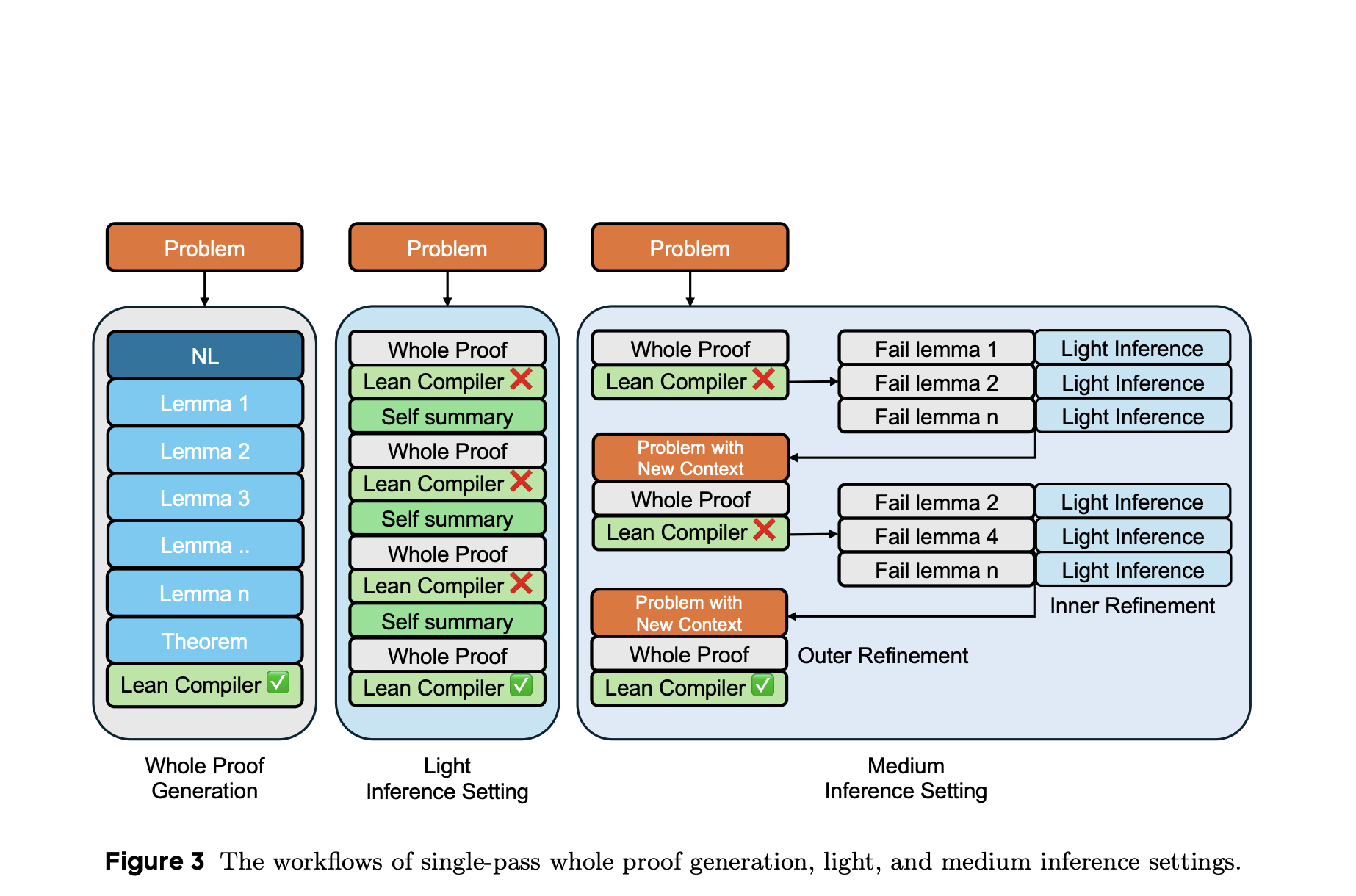
The Bytedance seed team presents Seed-Prover, a model of reasoning with the Lemma style test. He refines the evidence in an iterative manner using lightened feedback, previously established lemmas and the self-student. Seed-Prover uses three specialized test time inference strategies that allow deep and wide reasoning methods to solve IMO level competition problems. Its main innovation is to adopt in lemma style which proves as its main method, by placing lemms at the center of the reasoning process rather than counting on traditional methods of generation step by step or entirely waterproof. In addition, this article introduces the geometry of the seeds, an additional geometric reasoning engine which surmounts the limits of Lean in the management of the geometric support.
For the interaction between the seed prosecutor and the lean, in several stages, a multi-tasted RL based on VAPO is used. The training data set combines open source data sets with internal formal problems, using a proponent to create simpler variants of difficult tasks. It excludes too simple problems with evidence above 25%. The backend of seed geometry supports the generation of large -scale problems, identifying more than 230 million unique problems over seven days with an improvement of eight times in the efficiency of research. A distinct policy and value model is formed, although in -depth tests show that value models can reduce performance due to estimation errors. Consequently, the generation step by step with beam search is adopted in distributed configurations.
Seed-Prover obtains tip results on several mathematical landmarks. For the OMI 2025, the seed seeds fully solves 5 problems out of 6, with the seed geometry by instantly solving the problem 2 and deriving evidence for the remaining problem using various inference parameters. On OMI's previous problems, it turned out to be 121 out of 155 tasks, reaching a success rate of 78.1% at all levels of difficulty. The distribution of performance shows solid results between the categories of problems: solving 47 out of 55 easy problems, 47 out of 56 average problems and 27 difficult problems out of 44, with specific success rates, including 72 out of 85 in algebra, 42 out of 55 in number and 7 out of 14 in combinatorics.
On Minif2F, researchers reach a 99.6% proof rate for validation and testing sets in average parameters, solving difficult problems such as the IMI 1990 p3. Putnambench's results show an improvement from 201 to 331 problems resolved out of 657 when upgrading light to medium inference parameters, showing a significant performance jump compared to mathematical reasoning systems in the previous first cycle. On Combibench, the seed prosecutor solves 30 over 100 combinatorial problems, surpassing existing methods but revealing continuous challenges in combinatorial reasoning. Researchers achieved a success of 81.8% on MINICTX-V2, showing a strong generalization beyond competition problems and outperforming the 44.3% of the basic O4-Mini basic line at Pass @ 8.
In conclusion, Bytedance Seed presents the geometry of seeds and the prosecutor of seeds, two formal reasoning methods which integrate the capacities of LLM. The geometry of seeds provides an accelerated verification and improved search mechanisms while the seed prosecutor uses iterative refinement and complex test time inference strategies. The achievement of the resolution of 5 problems out of 6 in the OMI 2025 shows the practical effectiveness of these methods to combat elite mathematical competitions. The adoption of formal languages like Lean provides rapid verification of evidence which is more profitable than human experts and more reliable than LLM judges. Future research will focus on the combination of formal systems with LLM to resolve open conjectures.
Discover the Paper And GitHub page. Do not hesitate to consult our GitHub page for tutorials, codes and notebooks. Also, don't hesitate to follow us Twitter And don't forget to join our Subseubdredit 100k + ml and subscribe to Our newsletter.
Sajjad Ansari is a last year's first year of the Kharagpur Iit. As a technology enthusiast, he plunges into AI's practical applications by emphasizing the understanding of the impact of AI technologies and their real implications. It aims to articulate complex AI concepts in a clear and accessible way.