In the world of artificial intelligence, the role of in -depth learning becomes central. The paradigms of artificial intelligence have traditionally been inspired by the functioning of the human brain, but it seems that in -depth learning has exceeded the learning capacities of the human brain at certain aspects. Deep Learning has undoubtedly made impressive progress, but it presents its drawbacks, including high calculation complexity and the need for large amounts of data.
In light of the above concerns, scientists at Bar-Ilan University in Israel are raising an important question: should artificial intelligence integrate in-depth learning? They presented their new paperpublished in the journal Scientific Reports, which continues their Previous research On the advantage of architectures in the form of trees on convolutional networks. The main objective of the new study was whether complex classification tasks can be formed effectively using less deep neural networks based on principles of brain inspiration, while reducing the calculation load. In this article, we will describe key results that could reshape the artificial intelligence industry.
Thus, as we already know, the successful resolution of complex classification tasks requires training of deep neurons networks, made up of tens or even hundreds of convolutionary and fully connected hidden layers. This is very different from the functioning function of the human brain. In depth learning, the first convolutional layer detects the models located in the input data, and the following layers identify the models on a larger scale until a reliable class characterization of the input data is obtained.
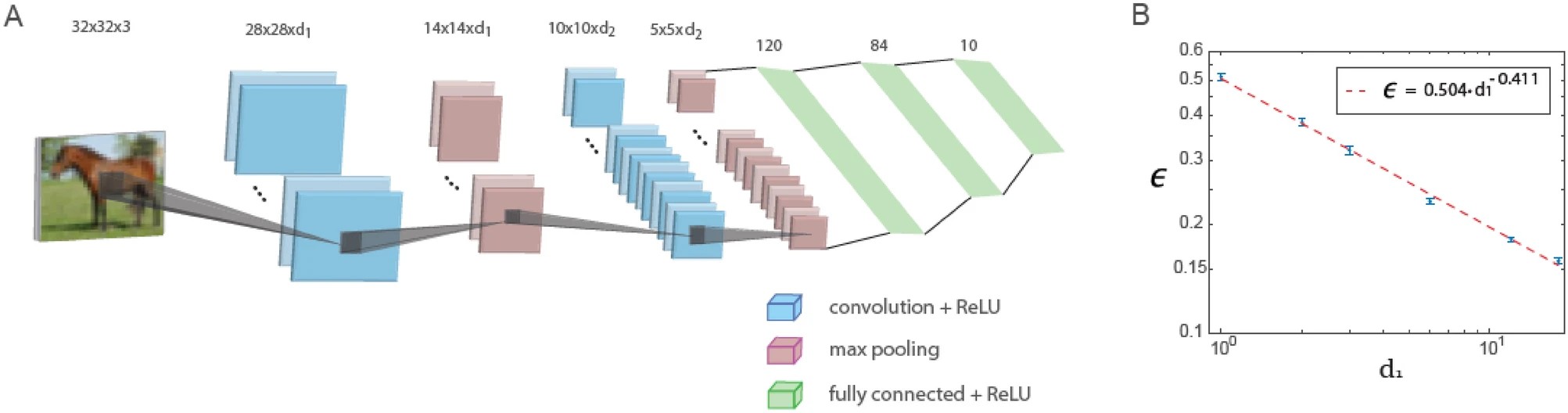
This study shows that when using a fixed depth report of the first and second convolutional layers, errors in a small lenet architecture consisting in just five layers decrease with the number of filters in the first convolutional layer according to a power law. The extrapolation of this power law suggests that the generalized lenet architecture is capable of obtaining low error values similar to those obtained with deep neural networks based on CIFAR-10 data.
The figure below shows training in a generalized lenet architecture. The generalized lenet architecture for the CIFAR-10 database (input size 32 x 32 x 3 pixels) consists of five layers: two convolutional layers using maximum accumulation and three fully connected layers. The first and second convolutional layers contain D1 and D2 filters, respectively, where D1 / D2 ≃ 6/16. The layout of the test error indicated ϵ, versus D1 on a logarithmic scale, indicating dependence on the power law with an exhibitor ρ∼0.41. The neurons activation function is reread.
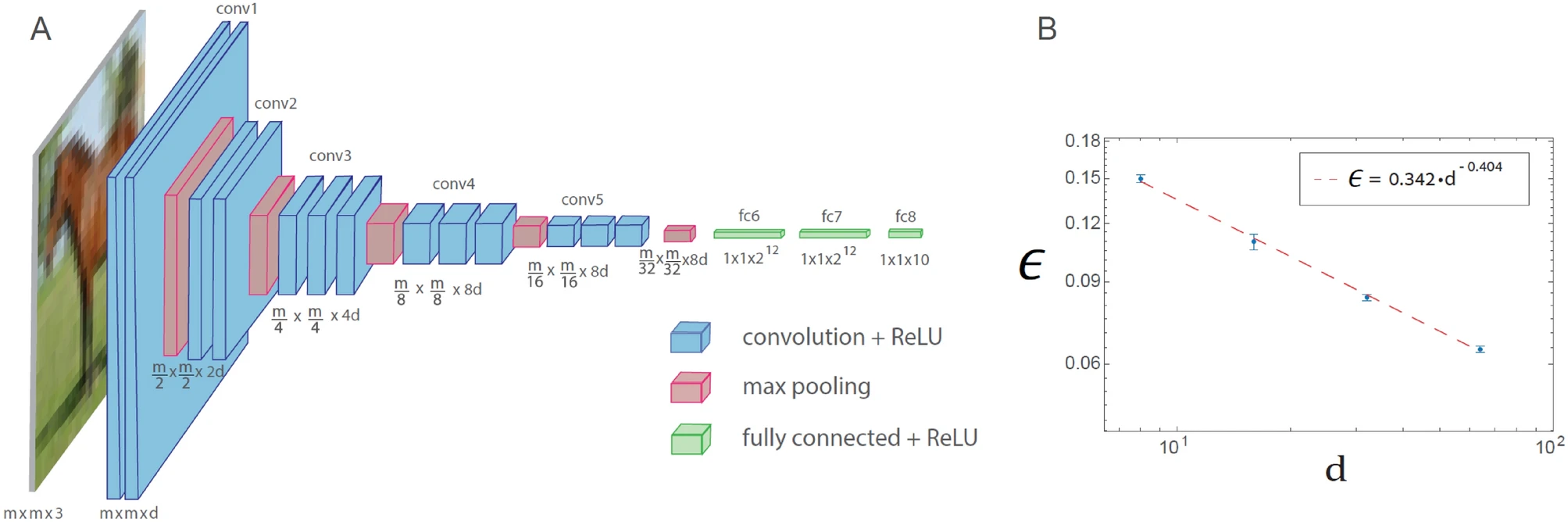
A phenomenon of law of similar power is also observed for generalized VGG-16 architecture. However, this leads to an increase in the number of operations necessary to achieve a given error rate compared to Lenet.
The generalized VGG-16 architecture training is demonstrated in the figure below. The generalized VGG -16 architecture composed of 16 layers, where the number of filters in the nth set of convolutions is DX 2N – 1 (n ≤ 4), and the square root of the filter size is MX 2 – (n – 1) (n ≤ 5), where MXMX 3 is the size of each entry (D = 64 in the original VGG -16 architecture). Plot of the test error, indicated ϵ, versus D on a logarithmic scale for the CIFAR-10 database (M = 32), indicating an addiction to the power law with an exhibitor ρ∼0.4. The neurons activation function is reread.
The phenomenon of the law of power covers various architectures Lenet and VG-16 generalized, indicating its universal behavior and suggesting a quantitative hierarchical complexity in automatic learning. In addition, the conservation law of convolutional layers equal to the square root of their size multiplied by their depth asymptotically minimizing errors. The effective approach to surface learning demonstrated in this study requires an additional quantitative study using different databases and architectures, as well as its accelerated implementation with future specialized material conceptions.