Mathematical reasoning has long been a great challenge for AI, not only demanding an understanding of abstract concepts but also the ability to make logical deductions in several stages with precision. Traditional language models, although capable of generating fluid text, often fight when responsible for solving complex mathematical problems which require both a deep knowledge of the domain and structured reasoning. This gap has motivated research to specialized architectures and training regimes designed to impregnate models with robust mathematical capacities. By focusing on targeted data sets and fine adjustment strategies, AI developers aim to fill the gap between understanding natural language and formal resolution of mathematical problems.
Nvidia introduced Openmath-nemotron-32B And Openmath-nemotron-14b-KaggleEach meticulously designed to excel in mathematical reasoning tasks. Based on the success of the Qwen family of transformer models, these Nemotron variants use a large -scale fine adjustment on a large corpus of mathematical problems, collectively known as the Openmatherason dataset. The design philosophy underlying the two libers focuses on the maximization of precision through competitive references while retaining practical considerations for the speed of inference and the efficiency of resources. By offering several sizes and configurations of models, NVIDIA offers researchers and practitioners a flexible toolbox to integrate advanced mathematical capabilities in various applications.
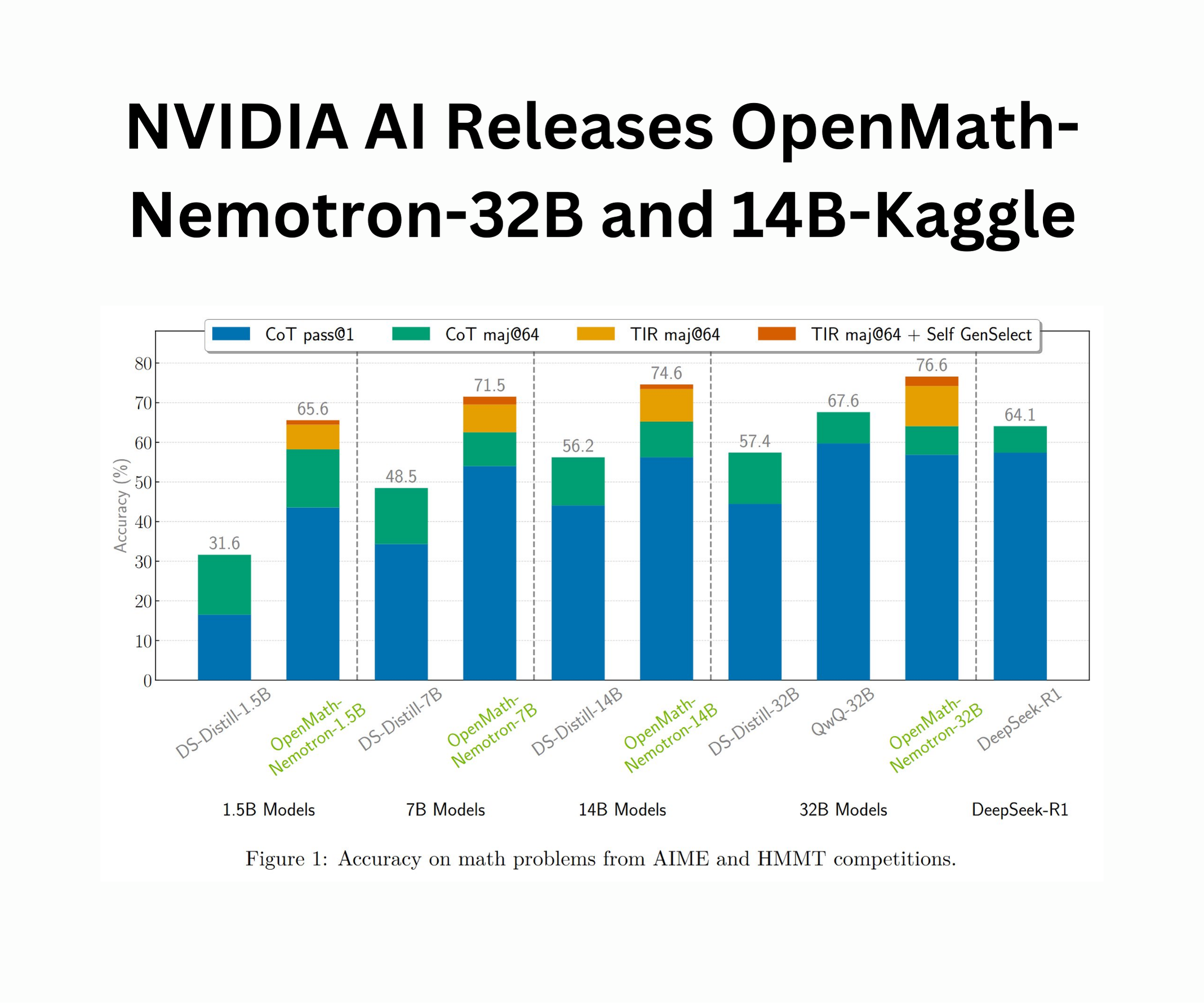
Openmath-nemotron-32B represents the flagship product of this series, with 32.8 billion parameters and taking advantage of BF16 tensor operations for effective material use. It is built by the END QWEN2.5-32B adjustment on the OpenMathreason data set, an organized collection that emphasizes difficult problems taken from mathematical Olympiads and standardized exams. This model obtains cutting -edge results on several rigorous references, notably the American Invitational Mathematics Examination (AIM) 2025 and 2025, the Harvard – Mathematics Tournament (HMMT) 2025-25, and the Mathematics series (Hle -Math) by Harvard – London – Edinburgh Examination (Hle -Math). In its reasoning configuration integrated into the tools (shooting), openmath-nemotron-32B obtains an average pass at @ 1 score of 78.4% on AIME24, with mainly 93.3% voting precision, exceeding the most efficient models by notable margins.
To adapt to different inference scenarios, OpenMath-nemotron-32B supports three distinct modes: the reflection chain (COT), the reasoning integrated into the tool (shooting) and the selection of generating solutions (genenselect). In COT mode, the model generates intermediate reasoning stages before presenting a final response, reaching a @ 1 precision of 76.5% on AIME24. When increased by genenselect, which produces several candidates solutions and selects the most coherent response, the model performance improves more, reaching a remarkable precision of 93.3% on the same reference. These configurations allow users to balance between the richness of the explanations and the accuracy of precision, to address research environments which require transparency as well as production parameters that prioritize speed and reliability.
Completing the variant of 32 billion parameters, Nvidia has also published Openmath-nemotron-14b-Kaggle, a model of 14.8 billion parameters adjusted on a strategically selected subset of the Openmathreason data set to optimize for competitive performance. This version served as the cornerstone of the first Nvidia solution in the Aimo-2 Kaggle competition, a competition focused on automated problem-solving techniques for advanced mathematical challenges. By calibrating the training data to highlight the problems reflecting the format and difficulty of the competition, the 14B-Kaggle model has demonstrated exceptional adaptability, exceeding rival approaches and securing the higher classification position.
Performance references for Openmath-nemotron-14b-Kaggle reflect those of its larger counterpart, the model reaching a Pass @ 1 precision of 73.7% on AIME24 in COT mode and improving at 86.7% under the genense protocols. On the reference likes25, it reaches a success rate of 57.9% (majority at 64 out of 73.3%), and on HMMT-24-25, it reaches 50.5% (majority at 64 of 64.8%). These figures highlight the model's ability to provide high quality solutions, even with a more compact parameter imprint, which makes it well suited to scenarios where resource constraints or inference latency are critical factors.
The two openmath-nemotron models are accompanied by an open-source pipeline, allowing complete reproducibility of the data generation, training procedures and evaluation protocols. NVIDIA has integrated these workflows into its Nemo-Skills framework, providing reference implementations for COT, TIR and GENSElect inference modes. With examples of code extracts that show how to instantiate a transformer pipeline, configure Dtype mapping and devices, and analyze the model outputs, developers can quickly prototyper applications that question these models for step -by -step solutions or rationalized final responses.
Under the hood, the two models are optimized to perform effectively on NVIDIA GPU architectures, ranging from ampère to microarchitectures of the hopper, taking advantage of highly adjusted Cuda libraries and Tensorrt optimizations. For production deployments, users can serve models via triton inference server, allowing low -flow and high speed integrations in web services or lots of lots. The adoption of BF16 tensor formats establishes an ideal balance between digital accuracy and the imprint of memory, allowing these large-scale models to integrate into GPU memory constraints while retaining robust performance on various material platforms.
Several key dishes from the release of Openmath-nemotron-32B and Openmath-Nemotron-14b-Kaggle include:
- Nvidia's Openmath-NEmotron series tackles the long-standing challenge to equip language models with robust mathematical reasoning thanks to a fine targeted adjustment on the OpenMathreason data set.
- The variant of 32 B settings reaches advanced precision on landmarks as loves 24 /25 and HMMT, offering three modes of inference (COT, TIR, GENSELECT) to balance the wealth and accuracy of the explanations.
- The “Kaggle” model of 14 B-Paramters B, refined on a subset on competition, ensured first place in the Aimo-2 Kaggle competition while maintaining high pass @ 1 scores, demonstrating efficiency in a smaller imprint.
- The two models are fully reproducible via an open source pipeline integrated into the NVIDIA Nemo-Skills framework, with reference implementations for all inference modes.
- Optimized for NVIDIA GPUs (Amprere and Hopper), the models exploit BF16 tensor operations, CUDA libraries, Tensorrt and the triton inference server for low latency and high speed deployments.
- Potential applications include AI -centered tutoring systems, tools for preparing academic competition and integration into scientific IT work flows requiring formal or symbolic reasoning.
- Future guidelines could extend to advanced university mathematics, multimodal entries (for example, handwritten equations) and more strict integration with symbolic calculation engines to check and increase the solutions generated.
Discover the Openmath-nemotron-32B And Openmath-nemotron-14b-Kaggle. Also, don't forget to follow us Twitter And join our Telegram And Linkedin Group. Don't forget to join our 90K + ML Subdreddit.
Asif Razzaq is the CEO of Marktechpost Media Inc .. as a visionary entrepreneur and engineer, AIF undertakes to exploit the potential of artificial intelligence for social good. His most recent company is the launch of an artificial intelligence media platform, Marktechpost, which stands out from its in-depth coverage of automatic learning and in-depth learning news which are both technically solid and easily understandable by a large audience. The platform has more than 2 million monthly views, illustrating its popularity with the public.